문제설명
fibonacci(3)을 호출하면 다음과 같은 일이 일어난다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
- fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
- 두 번째 호출한 fibonacci(1)은 1을 출력하고 1을 리턴한다.
- fibonacci(0)은 0을 출력하고, 0을 리턴한다.
- fibonacci(2)는 fibonacci(1)과 fibonacci(0)의 결과를 얻고, 1을 리턴한다.
- 첫 번째 호출한 fibonacci(1)은 1을 출력하고, 1을 리턴한다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1)의 결과를 얻고, 2를 리턴한다.
1은 2번 출력되고, 0은 1번 출력된다. N이 주어졌을 때, fibonacci(N)을 호출했을 때, 0과 1이 각각 몇 번 출력되는지 구하는 프로그램을 작성하시오.
즉, 피보나치 수열을 이용해 0과 1의 출력 횟수를 구하시오
입력값
1. 테스트케이스 개수 T
2. N (0<= N <= 40)
출력값
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
예제 입력1
3
0
1
3
예제 출력1
1 0
0 1
1 2
예제 입력2
2
6
22
예제 출력2
5 8
10946 17711
풀이
# 시간초과!
def fibo(n) :
global zero, one
if n == 0 :
zero += 1
return 0
if n == 1 :
one += 1
return 1
return fibo(n-2) + fibo(n-1)
T = int(input())
for _ in range(T) :
N = int(input())
zero = one = 0
print(zero, one)- 처음엔 예시로 나왔던 C++ 피보나치와 비슷하게 풀어봤지만 역시나 시간초과
정답코드
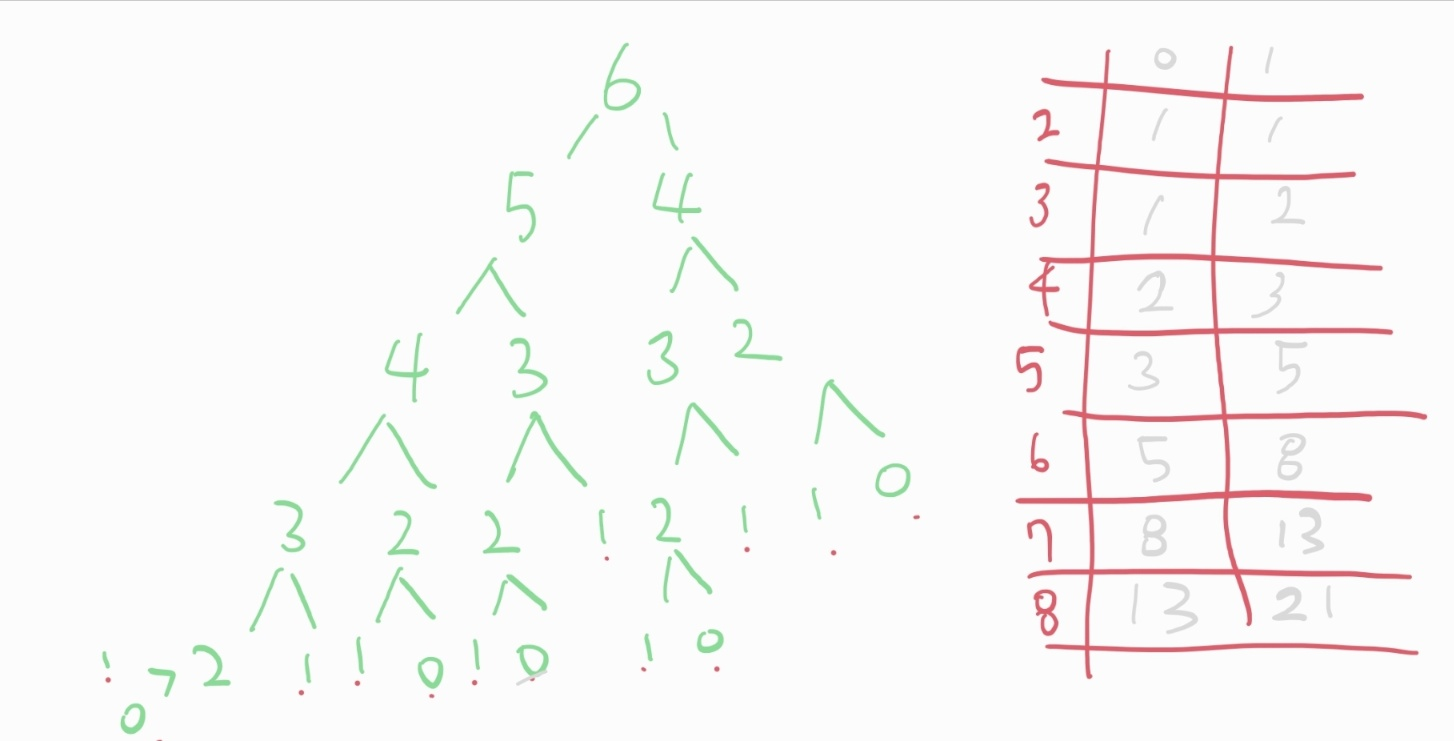
- 풀이를 보다가 0이 출력된 횟수는 fibo[N-1], 1이 출력된 횟수는 fibo[N]과 같다는 규칙을 발견함
- 또한 시간초과 문제를 해결하기 위해 dp 테이블 사용
# 110736KB, 108ms(PyPy3)
def fibo(n) :
if n == 0 :
return 0
if n == 1 or n == 2 :
return 1
if dp[n] != 0 :
return dp[n]
dp[n] = fibo(n-2) + fibo(n-1)
return dp[n]
T = int(input())
for _ in range(T) :
N = int(input())
dp = [0]*41
dp[1] = dp[2] = 1
if N == 0 :
print(1, 0)
else :
fibo(N)
zero = dp[N-1]
one = dp[N]
print(zero, one)- 기억나는대로 적었지만 코드가 지저분함
코드 개선
# 코드 개선
# 109544KB, 96ms(PyPy3)
T = int(input())
for _ in range(T) :
N = int(input())
dp = [0]*41
dp[1] = dp[2] = 1
if N == 0 :
print(1, 0)
else :
for i in range(3,41) :
dp[i] = dp[i-1] + dp[i-2]
zero = dp[N-1]
one = dp[N]
print(zero, one)- 불필요한 재귀함수 호출을 없애기 위해 반복문 사용함
- 메모리와 실행속도 측면에서 효율적임
코드 개선2
# 코드 개선
# 109544KB, 104ms(PyPy3)
# for문을 필요한 정도만 돌도록 수정했으나 유의미한 차이 없음
T = int(input())
for _ in range(T) :
N = int(input())
dp = [0]*41
dp[1] = dp[2] = 1
if N == 0 :
print(1, 0)
else :
for i in range(3,N+1) :
dp[i] = dp[i-1] + dp[i-2]
zero = dp[N-1]
one = dp[N]
print(zero, one)- for문을 필요한 정도(N)만 반복할 수 있도록 수정함
- 하지만 유의미한 차이가 없음
- 이유
- N의 범위가 작아서 반복 횟수 차이가 크지 않음
- 피보나치 수열은 단순 덧셈 연산으로 이루어져 연산 자체가 가벼움
- PyPy3는 JIT 컴파일러를 이용해 반복문을 효율적으로 처리함
'개발새발문제' 카테고리의 다른 글
| 백준 1991 트리순회 실버1 (0) | 2025.02.05 |
|---|---|
| 백준 9251 LCS 골드5(DP) (0) | 2025.01.11 |
| 백준 7569 토마토 골드5 (BFS) (0) | 2024.12.27 |
| 백준 30804 과일탕후루 실버2 (투포인터, defaultdict) (0) | 2024.12.26 |
| 백준 12865 평범한 배낭 (DP) (0) | 2024.12.18 |